Paint with prime numbers¶
A prime number which looks like salvador dali¶
number theorist
Prime numbers are ubiquitous. Prime numbers are fun. Prime numbers have many uses.
But the most important use of prime numners is in art. If you haven’t read prime numbers which look like giraffe, you should read it, but today we are doing something more fun. Finding prime numbers which look like famous artists.
We will use Salvador Dali, my favorite surrealist, as the guinea pig.
We will use the below striking image of Dali as our source image.

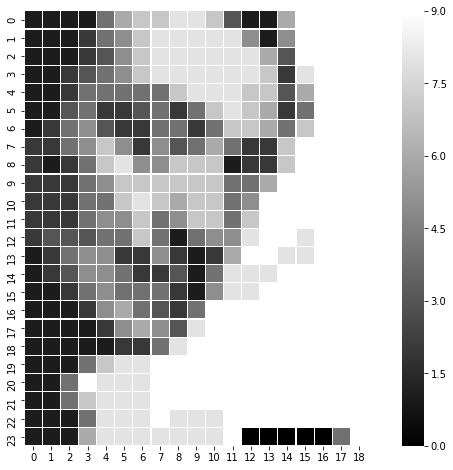
This is too large (on my machine) to parse as a number, so we will resize it to 24x24 grayscale image. It looks like this

Salvador Dali
Much smaller but still recognizable as Salvador. Lets get to work.
array([[1, 1, 1, 1, 4, 6, 7, 7, 8, 8, 7, 3, 1, 1, 6, 9, 9, 9, 9],
[1, 1, 1, 2, 4, 5, 7, 8, 8, 8, 8, 8, 5, 1, 5, 9, 9, 9, 9],
[1, 1, 1, 2, 3, 5, 7, 8, 8, 8, 8, 8, 8, 6, 3, 9, 9, 9, 9],
[1, 1, 2, 3, 4, 5, 7, 8, 8, 8, 8, 8, 8, 7, 2, 8, 9, 9, 9],
[1, 1, 2, 4, 4, 4, 4, 4, 7, 8, 8, 8, 7, 7, 3, 6, 9, 9, 9],
[1, 1, 3, 4, 2, 2, 3, 4, 2, 4, 7, 8, 7, 6, 2, 4, 9, 9, 9],
[1, 2, 4, 5, 3, 2, 2, 4, 4, 2, 4, 7, 7, 6, 4, 7, 9, 9, 9],
[2, 2, 4, 5, 7, 5, 2, 5, 3, 4, 6, 4, 2, 2, 7, 9, 9, 9, 9],
[2, 1, 2, 4, 7, 8, 5, 5, 7, 7, 7, 1, 2, 2, 7, 9, 9, 9, 9],
[2, 2, 2, 4, 5, 7, 7, 7, 7, 7, 7, 4, 4, 6, 9, 9, 9, 9, 9],
[2, 2, 2, 4, 4, 7, 8, 7, 6, 7, 7, 4, 5, 9, 9, 9, 9, 9, 9],
[2, 2, 2, 4, 5, 5, 7, 4, 5, 7, 7, 4, 7, 9, 9, 9, 9, 9, 9],
[2, 3, 3, 3, 4, 4, 7, 4, 1, 4, 5, 5, 8, 9, 9, 8, 9, 9, 9],
[1, 2, 4, 5, 5, 2, 2, 5, 2, 1, 2, 6, 9, 9, 8, 8, 9, 9, 9],
[1, 2, 3, 5, 5, 4, 2, 2, 3, 1, 4, 8, 8, 8, 9, 9, 9, 9, 9],
[1, 1, 2, 4, 5, 4, 4, 4, 2, 1, 5, 8, 8, 9, 9, 9, 9, 9, 9],
[1, 1, 1, 2, 5, 6, 4, 3, 2, 4, 9, 9, 9, 9, 9, 9, 9, 9, 9],
[1, 1, 1, 1, 2, 5, 6, 5, 3, 8, 9, 9, 9, 9, 9, 9, 9, 9, 9],
[1, 1, 1, 1, 1, 2, 2, 4, 8, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9],
[1, 1, 1, 4, 7, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9],
[1, 1, 4, 9, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9],
[1, 1, 4, 7, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9],
[1, 1, 1, 4, 8, 8, 8, 9, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9],
[1, 1, 1, 6, 8, 8, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9]])
111146778873116999911124578888851599991112357888888639999112345788888872899911244444788877369991134223424787624999124532244247764799922457525346422799992124785577712279999222457777774469999922244787677459999992224557457747999999233344741455899899912455225212699889991235542231488899999112454442158899999911125643249999999991111256538999999999111112248999999999911147889999999999991149888999999999999114788899999999999911148889888999999991116888888889999999
111146778873116999911124578888851599991112357888888639999112345788888872899911244444788877369991134223424787624999124532244247764799922457525346422799992124785577712279999222457777774469999922244787677459999992224557457747999999233344741455899899912455225212699889991235542231488899999112454442158899999911125643249999999991111256538999999999111112248999999999911147889999999999991149888999999999999114788899999999999911148889888999999991116888888890000049
<matplotlib.axes._subplots.AxesSubplot at 0x10e8cc978>
Slightly surreal, but still distinctly Salvador Dali. We have found the prime number
111146778873116999911124578888851599991112357888888639999112345788888872899911244444788877369991134223424787624999124532244247764799922457525346422799992124785577712279999222457777774469999922244787677459999992224557457747999999233344741455899899912455225212699889991235542231488899999112454442158899999911125643249999999991111256538999999999111112248999999999911147889999999999991149888999999999999114788899999999999911148889888999999991116888888890000049
Which when plotted in 2d looks like our Favorite Artist.
Populating the interactive namespace from numpy and matplotlib
/Users/shabda/.virtualenvs/yanny_vs_laurel/lib/python3.6/site-packages/IPython/core/magics/pylab.py:160: UserWarning: pylab import has clobbered these variables: ['number'] %matplotlib prevents importing * from pylab and numpy "n`%matplotlib` prevents importing * from pylab and numpy"

A prime number whose binary representation looks like a giraffe¶
Odd Number Theorists
First, here is a prime number whose binary representation is a T-Rex.
Math with bad drawings asked for a prime number whose binary representation is a giraffe. This lead to discussion on Math.reddit and Hacker news which led to finding such a prime number.
342581792649127676198127791406119644054852809184750511204770992210601825938383173228625368612512343524580568135765381129832784929140287102447656231670490278371618738040053550924844754083137995849927287014555199009052294292243605111352278964229602623894816760629354416193979550552423279842373621548435137856781153105076831681645952473068169294190544029391463758663828828100567003458546392021905815042131115480711892076216081858013250696070743624005842779807059777397154653840706692288630135185563366228931093496037459868457738024280865863648682544327375771172685872176976999577303715645442779935499071380556380855234358517399907184246818275843840363379983214925406281243183361618849192180391506653641933784053451121171160334712857092937535606122822893204604775038632348974223351004456787673186165100098223897371450275291114458983950607846718107603195397991880820766444935587675531082421404505700110617860358142315360174185418283092141238404865012380329781867103175076882601367389664213176688432343205501275425887396821357210158983064167712232404771958406106398750988506833703615072967113838953
You can see the binary representation on reddit.
As Nathaniel Borenstein said
It should be noted that no ethically-trained software engineer would ever consent to write a DestroyBaghdad procedure. Basic professional ethics would instead require him to write a DestroyCity procedure, to which Baghdad could be given as a parameter.
So the obvious next step is to generalize this is to program which can take an image and find a primary number whose binary representation is the image.
We run this for an Argentinosaurus image
python prime_dinosaur.py -f ~/Downloads/argentinosaurus.jpg -s 40
Which gives us
How does this work?¶
- We read the image and convert to desired size
- The image data is converted to monochrome and pixels darker (lower) than a threshold are converted 1, rest pixels are zero.
- This data is read in in a numpy array
- This 2d array is flattened, and treated as a bitarray to get a number
- We then start incrementing the number until we get a prime.
- The primality is tested using the Miller Rabin test.
- When such a number is found